Bob Jenkins's Small PRNG Passes PractRand (And More!)
I've been chatting on and off with David Blackman since August, 2017. Over our various conversations, I've gained huge respect for him and his contributions to random number generation over the last 15 years. In the course of a recent conversation I asked him about some of his favorite random number generators, and one of the ones he mentioned was A Small Noncryptographic PRNG by Bob Jenkins. Even though I had previously been aware of some of Bob Jenkins's other work regarding hash functions, somehow his work on noncryptographic random number generation fell through the cracks when I was surveying things that were out there back in 2014. I'll remedy that omission now.
Background
To my shame, it turns out I had missed a hugely influential work in the world of practical random number generation. In 1993 through 1995, Jenkins developed three generators designed to be cryptographically secure: IA, IBAA, and finally ISAAC. In an attempt to make a new smaller cryptographically secure generator, Jenkins developed FLEA, which eventually (with some insights from David Blackman) became his “A Small Noncryptographic PRNG”, first released on October 6, 2007.
Jenkins not only designed an interesting generator, but his website has insightful commentary on the design of PRNGs that is very worth reading. A few of his observations include
-
Generators based on random invertible mappings have much nicer properties than those based on random mappings. Random mappings have issues with bias (although if the generator is “too big to fail” that bias may not be detectable in practice), and poor cycle length. Designs based on random invertible mappings radically reduce these problems.
-
His discussion of “fast reversible primitives” shows similar ideas to the ones I used for permutation functions on tuples in PCG. It shows, as I long suspected, that although I came up with a nice name and a general way to present the idea, I was absolutely not the first person to discover this approach.
-
He also recommends “no nice math”. His point is that the more properties you can show mathematically about your PRNG scheme, the more likely it is to have too simple a structure, and that may lead to problems. Specifically, he does not like “mixing functions that spontaneously unmix”, which sounds to me like a dislike of issues like zeroland in LFSRs.
-
He also has a nice page on orders of magnitude which is useful for keeping perspective.
I wouldn't necessarily say that I agree 100% with every point Jenkins makes. Myself, I'm never impressed by “nice math” alone because a large number of generators with nice mathematical properties have proven themselves to have flaws of one kind or another, but I wouldn't necessarily outlaw “nice math” either. But I think Jenkins's negative opinion provides a very nice counterpoint to much of the established wisdom from those on the more academic and theoretical side of random number generation research, which oftentimes seems to value mathematical sophistication for its own sake.
Definitely worth a read.
Somewhat annoyingly, Jenkins doesn't seem to give this PRNG a name. It's descended from FLEA, so perhaps we should call it FLEA++, but I'll follow the naming convention used by Doty-Humphrey who called it JSF (Jenkins Small Fast) when he included it as a built-in generator in PractRand.
Design
Jenkins provides two variants of JSF, a 32-bit generator with 128 bits of state (internally stored as four 32-bit integers) and a 64-bit generator with 256 bits of state (internally stored as four 64-bit integers).
The form of the generator is the same across all versions, although whether a third rotate is used is optional (it is absent in the 32-bit version and present in the 64-bit version).
The 32-bit-output version, jsf32, is coded as
typedef uint32_t u4;
typedef struct ranctx { u4 a; u4 b; u4 c; u4 d; } ranctx;
#define rot32(x,k) (((x)<<(k))|((x)>>(32-(k))))
u4 ranval( ranctx *x ) {
u4 e = x->a - rot32(x->b, 27);
x->a = x->b ^ rot32(x->c, 17);
x->b = x->c + x->d;
x->c = x->d + e;
x->d = e + x->a;
return x->d;
}
void raninit( ranctx *x, u4 seed ) {
u4 i;
x->a = 0xf1ea5eed, x->b = x->c = x->d = seed;
for (i=0; i<20; ++i) {
(void)ranval(x);
}
}
and the 64-bit-output version, jsf64, is
typedef uint64_t u8;
typedef struct ranctx { u8 a; u8 b; u8 c; u8 d; } ranctx;
#define rot64(x,k) (((x)<<(k))|((x)>>(64-(k))))
u8 ranval( ranctx *x ) {
u8 e = x->a - rot64(x->b, 7);
x->a = x->b ^ rot64(x->c, 13);
x->b = x->c + rot64(x->d, 37);
x->c = x->d + e;
x->d = e + x->a;
return x->d;
}
void raninit( ranctx *x, u8 seed ) {
u8 i;
x->a = 0xf1ea5eed, x->b = x->c = x->d = seed;
for (i=0; i<20; ++i) {
(void)ranval(x);
}
}
(Note that in PractRand, jsf64 is a two-rotate variant using 39 and 11 for the two rotate constants. However Jenkins recommends the above three-rotate version for 64-bit use.)
Jenkins gives a lot of documentation for how the generator was designed, so I won't delve into that here, other than to say that it's very nice that he provides the tools he used in developing the magic constants. With a few changes, I was able to (hopefully correctly!) develop constants for similar smaller-sized versions, following my usual adage: always test a small one.
For 16-bit output with 64-bit state, I made jsf16 as follows
typedef uint16_t u2;
typedef struct ranctx { u2 a; u2 b; u2 c; u2 d; } ranctx;
#define rot(x,k) (((x)<<(k))|((x)>>(16-(k))))
u2 ranval( ranctx *x ) {
u2 e = x->a - rot(x->b, 13);
x->a = x->b ^ rot(x->c, 8);
x->b = x->c + x->d;
x->c = x->d + e;
x->d = e + x->a;
return x->d;
}
void raninit( ranctx *x, u2 seed ) {
x->a = 0x5eed, x->b = x->c = x->d = seed;
for (u2 i=0; i<20; ++i) {
(void)ranval(x);
}
}
and for 8-bit output with 32-bit state, I coded jsf8 as
typedef uint8_t u1;
typedef struct ranctx { u1 a; u1 b; u1 c; u1 d; } ranctx;
#define rot8(x,k) (((x)<<(k))|((x)>>(8-(k))))
u1 ranval( ranctx *x ) {
u1 e = x->a - rot8(x->b, 1);
x->a = x->b ^ rot8(x->c, 4);
x->b = x->c + x->d;
x->c = x->d + e;
x->d = e + x->a;
return x->d;
void raninit( ranctx *x, u1 seed ) {
x->a = 0xed, x->b = x->c = x->d = seed;
for (u1 i=0; i<20; ++i) {
(void)ranval(x);
}
}
The code above reflects the coding style used by Jenkins on his website, but for those of us that like to use PRNGs in C++, I've made the all of these generators available as jsf.hpp (a GitHub gist), which provides jsf64, jsf32, and more.
Standard Tests
I'll use PractRand to apply standard statistical tests. We could just test the standard versions of JSR, but I like to test smaller versions of random number generators because I consider 128-bit PRNGs to often be “too big to fail”. Whereas some people like to see generators pass tests, I prefer to get an understanding of where and when they fail. That way, we can have more confidence that when a large-state-space generator passes tests, it is not the case that failure is just over the horizon.
jsf8: 8-Bit Output / 32-Bit State
Any deterministic 32-bit-state generator must eventually fail statistical tests that demand a lot of data. The question is, how long can they go before they give out? In an ideal world, we might be able to produce nearly 232 8-bit outputs before the test suite detects an issue.
(It's worth noting that some authors in the literature claim that no should ever use more outputs than the square root of the period, which in this case would be a mere 64 kilobytes. But given that many generators continue to perform well for far longer than that, we will ignore this very conservative advice. If we followed it, many generators that fail statistical tests would pass.)
Let's take a look and see how jsf8 does
unix% ./jsf8 | ./RNG_test stdin8 -te 1 -tlmin 10 -tlmax 50 -tlmaxonly -multithreaded
# seed = 0x47
RNG_test using PractRand version 0.93
RNG = RNG_stdin8, seed = 0xdad66319
test set = expanded, folding = standard (8 bit)
rng=RNG_stdin8, seed=0xdad66319
length= 1 kilobyte (2^10 bytes), time= 0.2 seconds
no anomalies in 14 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 2 kilobytes (2^11 bytes), time= 0.6 seconds
no anomalies in 19 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 4 kilobytes (2^12 bytes), time= 1.1 seconds
no anomalies in 28 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 8 kilobytes (2^13 bytes), time= 1.6 seconds
no anomalies in 48 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 16 kilobytes (2^14 bytes), time= 2.8 seconds
no anomalies in 57 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 32 kilobytes (2^15 bytes), time= 3.7 seconds
no anomalies in 70 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 64 kilobytes (2^16 bytes), time= 4.7 seconds
Test Name Raw Processed Evaluation
[Low1/8]BCFN_FF(2+3):freq R= +7.7 p~= 8e-7 mildly suspicious
...and 82 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 128 kilobytes (2^17 bytes), time= 5.8 seconds
no anomalies in 92 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 256 kilobytes (2^18 bytes), time= 6.9 seconds
no anomalies in 102 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 512 kilobytes (2^19 bytes), time= 8.0 seconds
Test Name Raw Processed Evaluation
[Low1/8]FPF-14+6/16:cross R= +4.3 p = 1.1e-3 unusual
...and 113 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 1 megabyte (2^20 bytes), time= 9.1 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= -5.1 p =1-1.7e-3 unusual
...and 124 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 2 megabytes (2^21 bytes), time= 10.5 seconds
no anomalies in 136 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 4 megabytes (2^22 bytes), time= 11.9 seconds
no anomalies in 146 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 8 megabytes (2^23 bytes), time= 13.5 seconds
Test Name Raw Processed Evaluation
Gap-16:A R= -3.7 p =1-1.0e-3 unusual
...and 155 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 16 megabytes (2^24 bytes), time= 15.3 seconds
no anomalies in 166 test result(s)
rng=RNG_stdin8, seed=0xdad66319
length= 32 megabytes (2^25 bytes), time= 17.1 seconds
Test Name Raw Processed Evaluation
FPF-14+6/4:all R= -4.2 p =1-1.2e-3 unusual
...and 175 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 64 megabytes (2^26 bytes), time= 19.4 seconds
Test Name Raw Processed Evaluation
BCFN_FF(2+5,13-5,T) R= +10.5 p = 2.7e-4 unusual
FPF-14+6/4:all R= -5.8 p =1-2.8e-5 mildly suspicious
...and 182 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 128 megabytes (2^27 bytes), time= 22.1 seconds
Test Name Raw Processed Evaluation
FPF-14+6/32:all R= -4.3 p =1-1.0e-3 unusual
FPF-14+6/4:all R= -9.0 p =1-2.4e-8 very suspicious
[Low1/8]FPF-14+6/16:cross R= +4.8 p = 3.0e-4 unusual
...and 191 test result(s) without anomalies
rng=RNG_stdin8, seed=0xdad66319
length= 256 megabytes (2^28 bytes), time= 25.8 seconds
Test Name Raw Processed Evaluation
FPF-14+6/16:all R= -9.1 p =1-1.6e-8 very suspicious
FPF-14+6/16:all2 R= +8.3 p = 8.0e-5 unusual
FPF-14+6/4:(1,14-0) R= -8.7 p =1-9.4e-8 suspicious
FPF-14+6/4:(2,14-0) R= -8.2 p =1-2.7e-7 suspicious
FPF-14+6/4:(4,14-0) R= -6.9 p =1-4.4e-6 unusual
FPF-14+6/4:(5,14-0) R= -6.3 p =1-1.6e-5 unusual
FPF-14+6/4:(6,14-1) R= -7.9 p =1-1.7e-7 suspicious
FPF-14+6/4:all R= -19.4 p =1-1.1e-18 FAIL !
FPF-14+6/4:all2 R= +54.0 p = 3.2e-23 FAIL !!
...and 195 test result(s) without anomalies
We see here that everything was fine up until 226 bytes, when FPF-14+6/4:all began to become suspicious, finally failing the generator at 228 bytes.
In contrast, a 32-bit linear congruential generator outputting its highest (and best) 8-bits would begin to show signs of trouble at 220 bytes and fail at 223 bytes. For the question “is it better than an LCG?”, for this test the verdict is clear: yes.
However, if we contrast jsr8 against one of my favorite PRNGs, truncated XorShift*, it doesn't do so well. Truncated XorShift* makes it all the way out to 4 GB (232 bytes)—and then fails spectacularly at 8 GB because it completes its period at 4GB and begins repeating itself. We get similarly good results from the low 8 bits of pcg32_once_insecure.
So at this tiny size, jsf8 seems to be better than an LCG, but not as good as some other small generators. All in all, I see this result as encouraging. There is every reason to have good expectations for jsf16.
jsf16: 16-Bit Output / 64-Bit State
As we would hope, jsf16 performs quite well:
unix% ./jsf16 | ./RNG_test stdin16 -te 1 -tlmin 10 -tlmax 50 -tlmaxonly -multithreaded
# seed = 0xbf18
RNG_test using PractRand version 0.93
RNG = RNG_stdin16, seed = 0xc9575336
test set = expanded, folding = standard (16 bit)
rng=RNG_stdin16, seed=0xc9575336
length= 1 kilobyte (2^10 bytes), time= 0.2 seconds
no anomalies in 14 test result(s)
rng=RNG_stdin16, seed=0xc9575336
length= 2 kilobytes (2^11 bytes), time= 0.7 seconds
no anomalies in 19 test result(s)
[...]
rng=RNG_stdin16, seed=0xc9575336
length= 256 gigabytes (2^38 bytes), time= 4568 seconds
no anomalies in 492 test result(s)
rng=RNG_stdin16, seed=0xc9575336
length= 512 gigabytes (2^39 bytes), time= 9392 seconds
no anomalies in 506 test result(s)
rng=RNG_stdin16, seed=0xc9575336
length= 1 terabyte (2^40 bytes), time= 19024 seconds
no anomalies in 520 test result(s)
rng=RNG_stdin16, seed=0xc9575336
length= 2 terabytes (2^41 bytes), time= 37845 seconds
no anomalies in 534 test result(s)
rng=RNG_stdin16, seed=0xc9575336
length= 4 terabytes (2^42 bytes), time= 76688 seconds
no anomalies in 547 test result(s)
rng=RNG_stdin16, seed=0xc9575336
length= 8 terabytes (2^43 bytes), time= 158095 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= +6.1 p = 5.5e-3 unusual
...and 559 test result(s) without anomalies
rng=RNG_stdin16, seed=0xc9575336
length= 16 terabytes (2^44 bytes), time= 323804 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= +8.5 p = 8.5e-4 unusual
...and 572 test result(s) without anomalies
rng=RNG_stdin16, seed=0xc9575336
length= 32 terabytes (2^45 bytes), time= 609868 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= +13.6 p = 1.3e-5 suspicious
...and 584 test result(s) without anomalies
rng=RNG_stdin16, seed=0xc9575336
length= 64 terabytes (2^46 bytes), time= 1180621 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= +24.9 p = 1.7e-9 VERY SUSPICIOUS
[Low4/16]BCFN_FF(2+7,13-0,T) R= +9.7 p = 1.0e-4 unusual
...and 594 test result(s) without anomalies
rng=RNG_stdin16, seed=0xc9575336
length= 128 terabytes (2^47 bytes), time= 2302461 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= +46.8 p = 4.6e-17 FAIL !
...and 606 test result(s) without anomalies
We can see jsf16 fails fairly slowly. We see some suspicions developing at 243 bytes, but manage to reach 246 bytes without formally failing.
In contrast, a 64-bit linear congruential generator outputting its high 16 bits would start to show problems at 243 bytes and fail at 244 bytes. By 246 bytes it would have numerous FPF-test failures and be starting to fail the Gap test.
At this point, we can relax. If we have great statistical properties at 64 bits, we can have a strong expectation of passing with much larger state sizes and doing so with ample headroom.
jsf32: 32-Bit Output / 128-Bit State
As you might expect at this point, jsf32 does fine. Here's the full run:
./jsf32 | ./RNG_test stdin32 -te 1 -tlmin 10 -tlmax 50 -tlmaxonly -multithreaded
# seed = f8da1e08
RNG_test using PractRand version 0.93
RNG = RNG_stdin32, seed = 0x9c10fc42
test set = expanded, folding = standard (32 bit)
rng=RNG_stdin32, seed=0x9c10fc42
length= 1 kilobyte (2^10 bytes), time= 0.2 seconds
no anomalies in 14 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 2 kilobytes (2^11 bytes), time= 0.7 seconds
no anomalies in 19 test result(s)
[...]
rng=RNG_stdin32, seed=0x9c10fc42
length= 256 gigabytes (2^38 bytes), time= 3863 seconds
no anomalies in 479 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 512 gigabytes (2^39 bytes), time= 8103 seconds
no anomalies in 502 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 1 terabyte (2^40 bytes), time= 16133 seconds
no anomalies in 515 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 2 terabytes (2^41 bytes), time= 32103 seconds
no anomalies in 529 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 4 terabytes (2^42 bytes), time= 65677 seconds
no anomalies in 543 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 8 terabytes (2^43 bytes), time= 130780 seconds
no anomalies in 555 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 16 terabytes (2^44 bytes), time= 262377 seconds
no anomalies in 568 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 32 terabytes (2^45 bytes), time= 571682 seconds
no anomalies in 581 test result(s)
rng=RNG_stdin32, seed=0x9c10fc42
length= 64 terabytes (2^46 bytes), time= 1122137 seconds
Test Name Raw Processed Evaluation
DC6-9x1Bytes-1 R= -4.7 p =1-6.6e-3 unusual
[Low8/32]FPF-14+6/4:all R= -4.4 p =1-7.5e-4 unusual
...and 590 test result(s) without anomalies
rng=RNG_stdin32, seed=0x9c10fc42
length= 128 terabytes (2^47 bytes), time= 2251191 seconds
no anomalies in 603 test result(s)
Had I not tested at smaller sizes, I would be able to make a very clear judgement about statistical quality (because 128-bit PRNGs are often too big to fail tests), but since we have run smaller versions, we can feel much more confident that this version is great.
jsf64: 64-Bit Output / 256-Bit State
As you might expect at this point, jsf64 also does fine:
./jsf64 | ./RNG_test stdin64 -te 1 -tlmin 10 -tlmax
50 -tlmaxonly -multithreaded
# seed = 31a8a5a913716d9f
RNG_test using PractRand version 0.93
RNG = RNG_stdin64, seed = 0x8711fe3
test set = expanded, folding = standard (64 bit)
rng=RNG_stdin64, seed=0x8711fe3
length= 1 kilobyte (2^10 bytes), time= 0.3 seconds
Test Name Raw Processed Evaluation
FPF-14+6/32:all R= -15.3 p~= 1-4e-4 mildly suspicious
...and 13 test result(s) without anomalies
rng=RNG_stdin64, seed=0x8711fe3
length= 2 kilobytes (2^11 bytes), time= 0.8 seconds
no anomalies in 19 test result(s)
[...]
rng=RNG_stdin64, seed=0x8711fe3
length= 256 gigabytes (2^38 bytes), time= 3821 seconds
no anomalies in 629 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 512 gigabytes (2^39 bytes), time= 7951 seconds
no anomalies in 648 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 1 terabyte (2^40 bytes), time= 15919 seconds
no anomalies in 675 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 2 terabytes (2^41 bytes), time= 31643 seconds
no anomalies in 693 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 4 terabytes (2^42 bytes), time= 64409 seconds
no anomalies in 711 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 8 terabytes (2^43 bytes), time= 130798 seconds
Test Name Raw Processed Evaluation
[Low1/64]DC6-6x2Bytes-1 R= -4.6 p =1-2.4e-3 unusual
...and 728 test result(s) without anomalies
rng=RNG_stdin64, seed=0x8711fe3
length= 16 terabytes (2^44 bytes), time= 296202 seconds
no anomalies in 746 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 32 terabytes (2^45 bytes), time= 570029 seconds
no anomalies in 763 test result(s)
rng=RNG_stdin64, seed=0x8711fe3
length= 64 terabytes (2^46 bytes), time= 1158447 seconds
no anomalies in 779 test result(s)
Specialized Tests
Given my interest in understanding generators based on random mappings (especially SplitMix's split() function which creates a random mapping), it's useful to apply the same tools to understanding a small version of JSF.
Testing: jsf8: void advance() { rng.next();}
Finding cycles...
- state 00000000 -> new cycle 1, size 1, at 00000000 after 0 steps
- state 00000001 -> new cycle 2, size 2302945303, at 00000001 after 0 steps
- state 00000002 -> new cycle 3, size 1721638461, at 00000002 after 0 steps
- state 00000007 -> new cycle 4, size 116754811, at 00000007 after 0 steps
- state 00000032 -> new cycle 5, size 39480458, at 00000032 after 0 steps
- state 00000093 -> new cycle 6, size 86640801, at 00000093 after 0 steps
- state 000000a9 -> new cycle 7, size 14257782, at 000000a9 after 0 steps
- state 00000264 -> new cycle 8, size 4434647, at 00000264 after 0 steps
- state 000002f7 -> new cycle 9, size 3535831, at 000002f7 after 0 steps
- state 000004e7 -> new cycle 10, size 2676986, at 000004e7 after 0 steps
- state 00000bcc -> new cycle 11, size 2281180, at 00000bcc after 0 steps
- state 000053b4 -> new cycle 12, size 244833, at 000053b4 after 0 steps
- state 0000dc38 -> new cycle 13, size 33304, at 0000dc38 after 0 steps
- state 00010333 -> new cycle 14, size 21874, at 00010333 after 0 steps
- state 000383ca -> new cycle 15, size 8557, at 000383ca after 0 steps
- state 0004f83c -> new cycle 16, size 11981, at 0004f83c after 0 steps
- state 000b8b1a -> new cycle 17, size 35, at 000b8b1a after 0 steps
- state 00219eee -> new cycle 18, size 194, at 00219eee after 0 steps
- state 0056200b -> new cycle 19, size 174, at 0056200b after 0 steps
- state 03d52b26 -> new cycle 20, size 60, at 03d52b26 after 0 steps
- state 353008f4 -> new cycle 21, size 2, at 353008f4 after 0 steps
- state 427954c1 -> new cycle 22, size 10, at 427954c1 after 0 steps
- state 5466dd88 -> new cycle 23, size 4, at 5466dd88 after 0 steps
- state 82b1cc77 -> new cycle 24, size 3, at 82b1cc77 after 0 steps
- state 9cec8053 -> new cycle 25, size 3, at 9cec8053 after 0 steps
- state b4ad61bb -> new cycle 26, size 1, at b4ad61bb after 0 steps
Cycle Summary:
- Cycle 1, Period 1, Feeders 0
- Cycle 2, Period 2302945303, Feeders 0
- Cycle 3, Period 1721638461, Feeders 0
- Cycle 4, Period 116754811, Feeders 0
- Cycle 5, Period 39480458, Feeders 0
- Cycle 6, Period 86640801, Feeders 0
- Cycle 7, Period 14257782, Feeders 0
- Cycle 8, Period 4434647, Feeders 0
- Cycle 9, Period 3535831, Feeders 0
- Cycle 10, Period 2676986, Feeders 0
- Cycle 11, Period 2281180, Feeders 0
- Cycle 12, Period 244833, Feeders 0
- Cycle 13, Period 33304, Feeders 0
- Cycle 14, Period 21874, Feeders 0
- Cycle 15, Period 8557, Feeders 0
- Cycle 16, Period 11981, Feeders 0
- Cycle 17, Period 35, Feeders 0
- Cycle 18, Period 194, Feeders 0
- Cycle 19, Period 174, Feeders 0
- Cycle 20, Period 60, Feeders 0
- Cycle 21, Period 2, Feeders 0
- Cycle 22, Period 10, Feeders 0
- Cycle 23, Period 4, Feeders 0
- Cycle 24, Period 3, Feeders 0
- Cycle 25, Period 3, Feeders 0
- Cycle 26, Period 1, Feeders 0
- Histogram of indegrees of all 4294967296 nodes:
1 4294967296
- Histogram of the 256 allowed seeds to their cycles:
130 Cycle 2 (1, 2, 4, 6, 9, 10, 11, 12, 14, 17, ...)
112 Cycle 3 (0, 3, 5, 7, 8, 13, 15, 16, 18, 20, ...)
5 Cycle 4 (121, 177, 180, 233, 235)
2 Cycle 5 (99, 135)
4 Cycle 6 (67, 69, 132, 181)
2 Cycle 7 (90, 167)
1 Cycle 11 (173)
Because my cycle finder was designed for random mappings, it takes note of how long it takes to reach a cycle and what the in-degree of each node is. But for a random invertible mapping, all nodes are on a cycle so there are no “feeder” nodes leading to the cycles, and each node has an in-degree of 1. But it's nice to have those properties confirmed.
These results show that 93.7% of nodes lie on the two largest cycles. There are, however, some very short cycles and some moderately small cycles. If seeded using its provided seeding scheme, jsf8 will never be seeded into a very short cycle, although one seed does land in a cycle more than 1000 times smaller than the largest cycle.
For the larger-sized versions, the chances of accidentally landing on a small cycle become vanishingly small, and Jenkins has explicitly checked jsf32 to make sure that all allowed seedings lead to a reasonable-length cycle. In my next post, I do a little more analysis to confirm that there really is absolutely nothing to worry about.
In a very technical sense, we could say that the short cycles lead to a kind of bias (because the values they produce will never be observed for any non-pathological seeding). But this bias is vanishingly small.
Visualizing Zeroland
Generators based around xor, rotations, addition, and subtraction tend to have issues with low–hamming-weight states. In particular, rotating zero gives you zero, and zero as an argument to addition, subtraction, or xor is the identity function. As a result, we have a phenomenon known as zeroland in the state space of some PRNGs (it's also why these PRNGs disallow all-zeros initializations—they'd stay stuck at zero forever).
So let's examine how Jenkins's scheme behaves around these low–hamming-weight states. We'll examine the state space of jsf64, looking at points where the state space crosses a minimal–hamming-weight state where only a single bit is set.
Here's a sample of six moments where the generator crosses a minimal-hamming-weight state. In each case, each row of the randogram represents the 256-bit internal state of the generator. Each subsequent row in the picture represents the next internal state. The middle of the picture is where it passes through a mostly-zeros state.
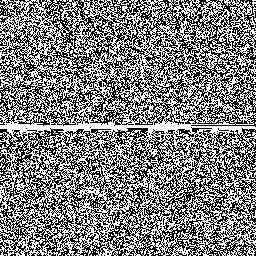
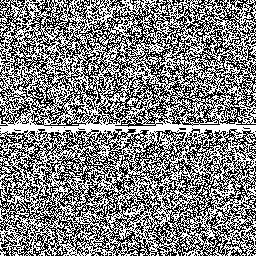

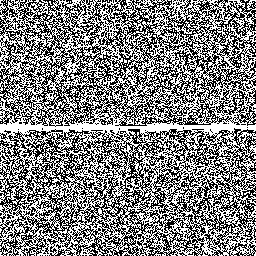

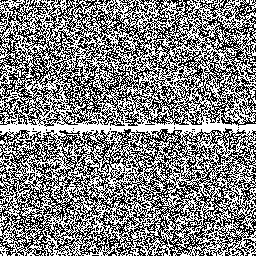
There are only 256 states with minimal hamming weight, but there are quite a lot of other low–hamming-weight states. For example, there are about 248.5 states with only eight bits set. Here's the generator crossing a few of those:
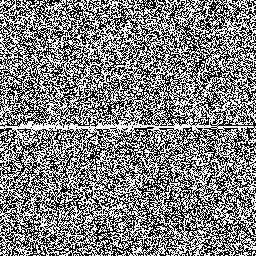
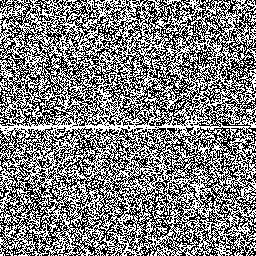

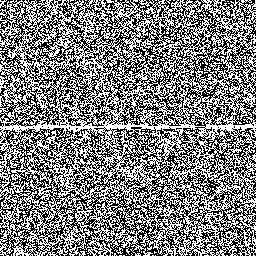
Overall, although these glitches don't look very nice and are a little bit improbable, we can see that they're fairly modest and are unlikely to be easily detected in practice.
As an aside, not every generator has these kinds of glitches as it crosses an all-zeros state. These two diagrams show a 256-bit LCG and MCG as they cross a minimal–hamming-weight state. We can see that the states before and after are unaffected (but note the weak low-order bits over on the righthand edge).
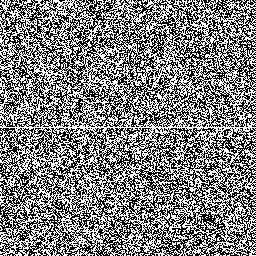
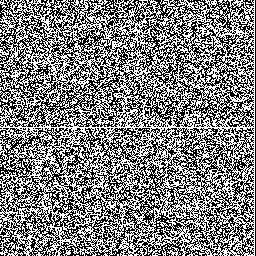
Speed
Lately I've been using Vigna's hamming-weight test as a quick and easy speed benchmark (although I've adjusted his code to use gettimeofday() rather than time() for more accurate timing).
Compiling with Clang, I see
processed 1.75e+11 bytes in 41.6 seconds (4.21 GB/s, 15.16 TB/h). Sat May 26 21:25:05 2018
and with GCC, I see
processed 1.75e+11 bytes in 43.8 seconds (3.998 GB/s, 14.39 TB/h). Sat May 26 21:27:16 2018
Seems nicely fast. Not quite as fast as an MCG (if you're using Clang), but faster than PCG and Xoshiro256**. Which is great considering it's a design that's more than ten years old.
Predictability
JSF isn't intended to be cryptographically secure, but it is certainly annoying to predict, in part due to Jenkins's “no nice math” rule. My usual methods are about a million times slower predicting this generator than they are for trivially predictable generators such as SplitMix, Xoroshiro, or Xoshiro.
As a test, I investigated whether a jsf32 generator could ever produce the output 1, 2, 3, 4. A little over five days later I had my answer—it can't. Then I somewhat arbitrarily searched for a state that would produce the numbers 0x52ddff94, 0xb3a7faf3, 0x5e70c6e9, 0xa0796e44. Nearly three days later I had (re)discovered the state that would produce these outputs, { 0xc698f9ba, 0x129692a7, 0x94646b27, 0xc1c8ca84 }. In my eyes, I got lucky because there may be multiple states that could produce this sequence, and I happened to find the one I'd used to create these values in the first place.
Very probably there may be more advanced techniques than the ones I used (because mine required little thought or effort on my part), but to me this generator sits squarely in the middle ground of prediction difficulty. Not 100% trivial, but absolutely not cryptographically secure. Clearly we're doing vastly better than brute force, where we'd simply guess 96 unknown bits, taking billions of years to do so. But although on a cosmic scale, a few days of computation is nothing, it's sufficiently annoying to make various kinds of algorithmic complexity attacks more trouble to mount than they cause.
Interestingly, Jenkins also provides a JSF variant with an extension array that is accessed based on other parts of the PRNG state (somewhat reminiscent of PCG's extension array but more integrated rather than as a bolted-on extra). He embraces the idea that it might be cryptographically secure, but if so, “only just”.
Other Features
JSF is light on other features. The “no nice math” rule means we cannot have certain nice things, like fast jump-ahead or a distance function. These absent features are unlikely to be much of a concern for most users.
Other Reviews
JSF is one of the generators that Doty-Humphrey explicitly reviews in the PractRand documentation, saying:
it is a good small fast chaotic RNG and it is better studied that other small fast chaotic RNGs. This algorithm was written by Bob Jenkins. This small fast RNG is what I use as my baseline for the category of small fast RNGs. This small fast RNG has an advantage over most in that a lot of people have looked at it, and many people have tried their own custom unpublished RNG tests on it. No biases have been reported in the ouput of the 32 or 64 bit versions of this. Even versions scaled down to 16 bits pass most tests.
Conclusion
I looked at this PRNG because it's a favorite of David Blackman, and I hugely respect his opinion. He mentioned to me that this generator helped spur a lot of recent development in random number testing as people tried (and failed) to break it.
It seems like at its standard sizes, JSF is very fast and it passes PractRand easily, and does so without needing operations such as multiplication that historically were not especially fast and even today aren't fast everywhere (although they are very fast with many recent CPUs, including x86 variants).
The biggest concern is the existence of short cycles. But all the data (and analysis) suggests that the chance of it being an issue is vanishingly small. Given the amount of scrutiny this generator has received over the years, I don't think there is a lot to worry about here. So feel free to use it if you feel like working with a generator that is fast, reasonably sized, and very well scrutinized.
Perhaps the most interesting thing about this generator is that it has inspired some other really good PRNGs that apply the same principles to make fast high-quality generators, but make short cycles completely impossible (by mixing in a counter). Examples of these PRNGs include Elias Yarrkov's v3b PRNG, David Blackman's gjrand, and Chris Doty-Humphrey's Small Fast Counting RNG (sfc).
About sfc, Doty-Humphrey writes:
This algorithm is [a] combination of very fast speed, good statistical properties, small size, and (on larger word sizes) guaranteed minimum cycle length. I wrote this algorithm. So I might be prejudiced.
This has not been as thoroughly tested as the
jsfalgorithm, but on my tests so far it appears superior tojsfin both quality and speed. It's basically a good small chaotic RNG driven by a bad smaller linear RNG. The combination gives it the strengths of each - good chaotic behavior, but enough structure to avoid short cycles.
I like that too! One more PRNG examined; so many more to look at!